Le projet OpenSolarMap démontre comment il est possible d’améliorer la connaissance du territoire français en utilisant astucieusement les ressources de la multitude et des data-sciences. Son objectif concret est de classifier les toitures en quatre catégories : orientation nord/sud; orientation est/ouest ; toit plat ; autre ou indéterminé. Cela permet, par exemple, d’évaluer le potentiel d’installation de panneaux solaires ou la possibilité de végétaliser. Quelques milliers d’exemples ont été recueillis grâce à une plateforme de crowdsourcing. Puis, des algorithmes ont été utilisés pour couvrir l’ensemble du territoire. Une présentation générale du projet est accessible sur le blog d’Etalab.

Cet article est le premier d’une série qui présente la partie data-science du projet. C’est l’occasion de brosser à grands traits la démarche du data-scientist et de faire le tour de quelques techniques fréquemment utilisées. La série vise avant tout un public technique mais non spécialiste. Des références permettent d’approfondir les notions survolées.

Le code source écrit pour le projet OpenSolarMap est accessible sur la plateforme GitHub. La partie data-sciences est contenue dans le repository solml.

Analyse des contributions

Nous avons voulu tout d’abord procéder à une analyse des contributions faites sur l’interface opensolarmap.org. Au 21 décembre 2014, nous disposions de 130.374 contributions, sur 38.553 bâtiments, permettant de classifier avec confiance 10.771 bâtiments par un système de vote. Ces contributions sont accessibles sur la plateforme data.gouv.fr.

L’interface de contribution ne connaît le contributeur que par son adresse IP. Cette adresse IP est ensuite hashée pour préserver l’anonymat. Les contributions proviennent de 1081 utilisateurs.

Mauvaises contributions

Certaines contributions portent sur des bâtiments dont on ne connait pas encore avec certitude la vraie classe. Pour faire une analyse des erreurs, il ne faut garder que les prédictions qui portent sur les bâtiments déjà classifiés. Ces contributions, dont on peut dire si elles sont justes ou fausses, sont au nombre de 60.436.

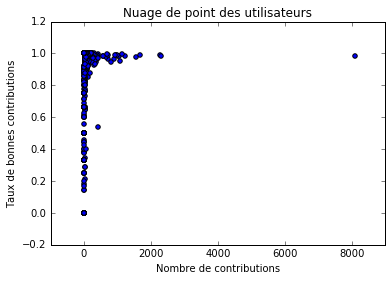
Figure 1

Parmi ces contributions, il y a 1.998 erreurs. Cela représente 3.3% des contributions. Il faut cependant noter que les bâtiments classifiés avec certitude sont en moyenne plus faciles à classifier que les autres. Les contributions sur ces bâtiments sont donc moins susceptibles d’ètre erronées. Le taux d’erreurs réel est donc sans doute plus élevé que cette valeur observée.

La figure 1 montre la répartition des utilisateurs suivant leur nombre de contributions et leur taux de contributions correctes. On ranger les contributeurs en plusieurs catégories : des contributeurs ayant un nombre de contributions élevé et un un taux de contributions correctes proche de 1. Dans cette catégorie, on remarque un contributeur ayant environ 8.000 contributions à lui seul : c’est Christian Quest ! des contributeurs ayant un nombre faible de contributions et un taux de contributions correctes faible. On peut faire l’hypothèse que ce sont des contributeurs n’ayant pas compris comment utiliser l’interface de contribution. un contributeur a quelques centaines de contributions et un taux faible, proche de 55%. L’analyse de ses contributions montrent qu’il s’agit sans doute d’un comportement malveillant. On peut ètre étonné de rencontrer ici un comportement malveillant, mais comme on va le voir tout de suite, il est très facile de s’en prévenir.

En ignorant les contributions des utilisateurs ayant un taux observé de contributions correctes de 70%, on peut éliminer 191 contributeurs pour 725 erreurs, c’est-à-dire plus d’un tiers des erreurs.

Influences sur le taux de contributions correctes

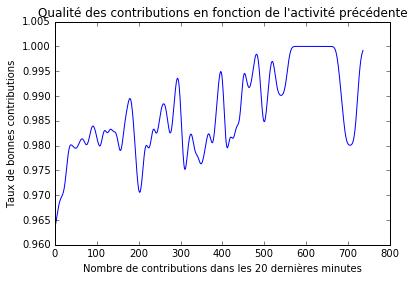
Figure 2

On peut se demander s’il existe des facteurs qui influencent le taux de contributions correctes.

Existe-t-il un effet de fatigue avec un taux de contributions correctes qui baisserait d’autant que le contributeur a contribué au cours de 20 dernières minutes ? La figure 2 indiquerait plutèt le contraire.

Quelle est l’influence du temps de réponse sur le taux de contributions correctes ? La figure 3 montre que ce taux est optimal entre 1 et 3 secondes environ. En dessous d’une seconde, il chute rapidement à 93% pour un temps d’environ 0.5 seconde. Dans ces cas, le contributeur n’a peut-ètre pas pris assez de temps pour répondre précisément. Au delà de 3 secondes il chute aussi. Le contributeur a peut-ètre hésité face à un bètiment plus difficile à classifier que la moyenne.

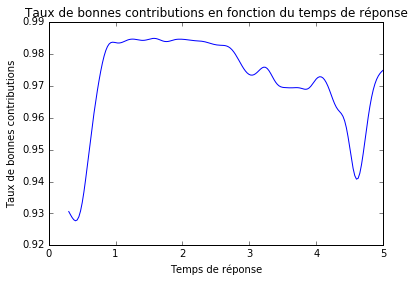
Figure 3

Entraéner un classifieur automatique

L’ensemble des bâtiments dont on connaét l’orientation grèce aux contributeurs est bien plus petit que le nombre total de bâtiments construits sur le territoire franéais. Mais il est possible d’automatiser une tache de classification, à la condition d’avoir un nombre suffisant d’exemples préalablement classifiés.

Pour simplifier le problème, on ne va s’attaquer dans un premier temps qu’aux deux premières classes : les toitures orientées au nord et au sud les toitures orientées à l’est et à l’ouest

De plus, ces deux classes seront de tailles égales, ce qui ne correspond pas à la réalité.

On verra dans plus tardécomment généraliser une solution à deux classes pour distinguer quatre classes de tailles inégales.

Flux de données

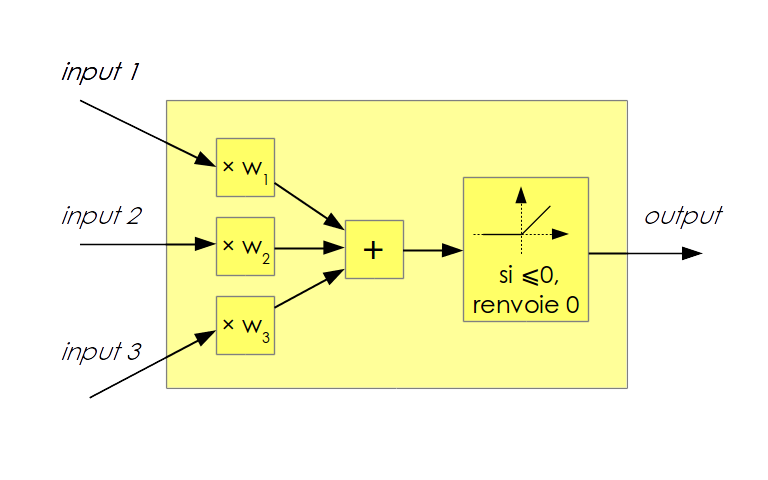
Voici la description du flux des données traitées, depuis les informations requètées depuis l’extérieur vers le résultat de la classification : Le cadastre est consulté via la base de donnée d’OpenStreetMap. Le cadastre contient le contour des murs extérieurs. Ce contour est simplifié en un rectangle. Le bètiment n’est pas examiné davantage si la toiture n’est pas susceptible d’ètre orientée au sud, c’est-é-dire si l’orientation du rectangle s’écarte trop des directions cardinales. L’image satellite des toits est requètée avec GDALésur l’API de Mapbox. GDAL est une excellente librairie de traitement d’images géospaciales. Dans ce projet, toutes les conversions entre référentiels géographiques et référentiels cartographiques sont gérées par GDAL. GDAL permet également d’aller chercher les images satellite des toits à partir des coordonnées voulues, et gère de manière transparente le requètage par internet, le découpage parétuiles et le cache. Après cette étape de téléchargement, les images satellites des toits sont stockées localement au format jpg. Une image est une grille de pixels de tailleévariableésouvent proche de 100 par 100. Chaque pixel est composée de 3 valeurs entières comprises entre 0 et 255 pour coder l’intensité des couleurs rouge, vert et bleu. Les images subissent une réduction de la taille et/ou un passage en noir et blanc suivant les besoins du classifieur. A l’issue de ce prétraitement, les images ont toutes la mème taille et le classifieur pourra traiter l’image comme un tableau numérique de taille fixée. Une image pourra ètre vue selon les cas comme un tableau à deux dimensions auquel cas la géométrie de l’image est préservée, ou comme un tableau à une dimension (un vecteur). Dans ce cas les valeurs de chaque pixel sont dépliées sur une seule dimension. On parle de « features » pour désigner ces valeurs numériques caractérisant une image. Un classifieur automatique intervient ici pour produireéun avis pour chaque toit. Cet avis se compose de l’indice de la classe jugée la plus probable et d’un indice de confiance. Ce score peut ensuite ètre reversé dans la base OpenStreetMap.

Un premier algorithme très simple

Par principe, nous commençons toujours nos analyses par un algorithme extrèmement simple. Cette étape est très importante pour ces raisons : Si ce premier algorithme, aussi simple qu’il soit, répond complètement au besoin initial, il n’y a pas de temps perdu à développer un autre modèle plus complexe. De manière générale, un algorithme est d’autant mieux accepté, rapide d’implémentation et d’exécution, maintenable et robuste qu’il est simple. Sinon, il fournit une base de comparaison pour d’autres algorithmes plus sophistiqués. En cas de calendrier serré ou de délai non anticipé durant le développement d’un algorithme mieux adapté, il constitue une solution de substitution immédiatement utilisable.

OpenSolarMap ne déroge pas à la règle. Une image de toit est divisée en 4 parties égales comme représenté sur le figure 4. Pour chacune de ces zones, on somme la valeur de chaque couleur de chaque pixel. On va noter ces sommes S1, S2, S3 et S4.

Figure 4

Puis à partir de ces sommes on calcule la différence entre la partie droite et la partie gauche de l’image, puis entre la partie haute et la partie base de l’image.

I�NS = |(S1+S2) ‘ (S3+S4)|
I�EW = |(S1+S3) ‘ (S2+S4)|

On peut s’attendre à ce que la première différence soit plus importante pour les toitures orientées est-ouest alors que la seconde différence soit plus importante pour les toitures orientées nord-sud. Calculons donc la différence entre ces deux différences :

Y = I�NS – I�EW + c

La constante c est introduite pour prendre en compte l’asymétrie causée par la position du soleil, toujours au sud, et de l’ombre, toujours au nord. Sa valeur est fixée pour maximiser la performance du modèle.

Le résultat de l’algorithme est le signe de Y. Si Y est positif, l’algorithme prédit une orientation nord-sud, si le signe est négatif il prédit une orientation est-ouest. Avec une valeur deéc optimale, le taux d’erreur est de 38%. C’est mieux que le classifieur aléatoire, qui répond 0 ou 1 avec une probabilité égale et qui a donc un taux d’erreur de 50%. Mais ce n’est pas satisfaisant. Il faut donc chercher un algorithme plus compliqué.